Geometrische Gruppentheorie
Die geometrische Gruppentheorie untersucht Gruppen, indem sie sie als geometrische Objekte mit einer Metrik behandelt. Dies kann für Gruppen geschehen, die endlich erzeugt sind, d.h. die aus einer endlichen Teilmenge durch Multiplikation und Inversion rekonstruiert werden können. Typische Beispiele sind Fundamentalgruppen von Mannigfaltigkeiten oder Gruppen von Matrizen mit ganzzahligen Koeffizienten.
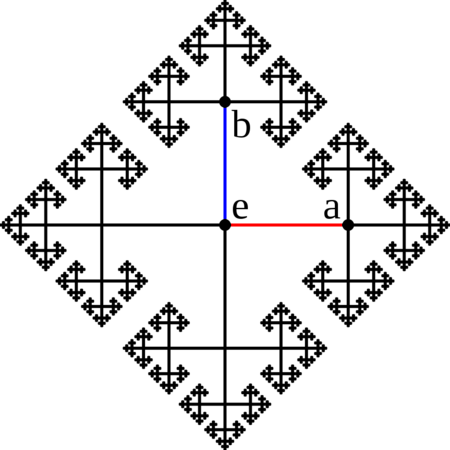
Ausgehend von einem endlichen Erzeugendensystem \(S\) einer Gruppe \(G\) kann man eine Metrik auf \(G\) definieren, indem man einen zusammenhängenden Graphen, den sogenannten Cayley-Graphen von \(G\), konstruiert, wobei \(G\) als Menge von Knoten aufgefasst wird und orientierte Kanten Elemente in \(G\) verbinden, die sich durch eine Rechtsmultiplikation mit einem Erzeuger von \(S\) unterscheiden. Ein Cayley-Graph hängt nicht nur von der Gruppe, sondern auch vom gewählten (endlichen) Erzeugendensystem ab. Quasi-Isometrie ist die entsprechende Äquivalenzrelation auf metrischen Räumen, die die Eigenschaft beschreibt, dass Cayley-Graphen, die auf verschiedenen Erzeugendensystemen basieren, gleich sind.
Unter den fundamentalen Fragen der geometrischen Gruppentheorie finden wir folgende:
1. Wenn \(G\) und \(H\) quasi-isometrische Gruppen sind, inwieweit haben \(G\) und \(H\) dieselben algebraischen Eigenschaften?
2. Wenn eine Gruppe \(G\) quasi-isometrisch zu einem metrischen Raum \(X\) ist, welche geometrischen Eigenschaften auf \(X\) übertragen sich auf interessante algebraische Eigenschaften?
Die geometrische Gruppentheorie entstand als eigenständiges Gebiet der Mathematik zwischen den 1980er und 1990er Jahren dank der Monographie "Hyperbolische Gruppen" von Mikhail Gromov, in welcher der Begriff der hyperbolischen Gruppen eingeführt wurde. Das Gebiet der geometrischen Gruppentheorie steht in engem Zusammenhang mit der niedrigdimensionalen Topologie, der hyperbolischen Geometrie, dem Studium der Lie-Gruppen und ihrer diskreten Untergruppen, der mathematischen Logik und anderen Bereichen der Mathematik und bietet ein wichtiges Instrumentarium zur Untersuchung topologischer Oberflächen und ihrer Automorphismengruppen.

